Snad každý zažil pocit, že mu mrak plující po čerstvě vymetené obloze, hromada kamenů, skalisko, nebo hora neodolatelně připomněly určitou věc nebo člověka. Všeobecnosti tohoto prožitku ostatně nasvědčuje místopis bližších i vzdálenějších oblastí, kde se to různými kamennými starci a stařenami, čerty a pannami jen hemží, nebo železná pravidelnost, se kterou lidé objevují na ubrouscích, toustech a kouscích pizzy svaté obrázky.

Jak je ale možné, že nás u některých tvarů mozek tak lehce ošálí? 

Jednoduché vysvětlení, že zmíněné a další věci přírodní útvary prostě připomínají, neobstojí. Jen trochu odlišné, podobně složité, exoticky tvarované a zdánlivě sugestivní přírodniny v nás totiž nemusí vyvolat představu vůbec ničeho.

Kápl na to Švýcar Rorschach

Psychický jev, při kterém domýšlíme neurčité nebo nejasné podněty do povědomých podob s pomocí fantazie, se nazývá pareidolie. Nejúspěšnějším případem profesionálního využití této lidské schopnosti je patrně Rorschachův test, který zná každý, kdo někdy zavadil o psychologii, nebo alespoň viděl film či seriál z tohoto prostředí. Jsou to dvoustraně souměrné inkoustové skvrny, ve kterých jeden člověk vidí buket květin, zatímco druhý třeba netopýra.

Herman Rorschach, švýcarský psycholog a psychiatr, který karty s inkoustovými obrázky na začátku dvacátých let minulého století vytvořil, svůj test pokládal za klíč k nejtajnějším částem lidského nevědomí.

Kůň převlečený za mrak. | zdroj: tisková zpráva

Někteří jeho současníci jej zase považovali za nástroj k odhalení všech psychických chorob. Rorschachův test se tak stal nejrozšířenějším psychologickým testem vůbec.

S postupem času původní vybičovaná očekávání poněkud odpadla. I největší skeptik dnes ale uznává hodnotu testu alespoň pro odhad individuální imaginace či kreativity.

Lidská schopnost vidět v náhodných skvrnách konkrétní věci, lidi a situace je každopádně fascinující. Pro každou kartu je zdokumentováno více než 300 různých interpretací!

Není divu, že podobný fígl s náhodnými skvrnami využívala a stále využívá i řada moderních umělců, od surrealistů po Andyho Warhola. Jaké vlastnosti ale daný objekt, ať už je to skvrna, oblak, nebo hromada kamenů, musí splňovat, abychom "v něm něco viděli"?

Fraktály, kam se podíváš

Dřívější výzkumy ukázaly, že stěžejní je fraktálový tvar kontury objektu. Fraktály jsou takové útvary, které se opakují ve stejné podobě na všech úrovních. Jinými slovy, jsou sobě podobné na všech škálách.

Není v tom ale nic mystického – tyto vlastnosti splňuje hned na několika úrovních například hlávka květáku, nebo krevní oběh či řeka, u kterých se nejsilnější proud skládá z řady menších přítoků, ty se slévají z ještě menších potůčků a tak dále.

Fraktálová struktura je přírodě vlastní. K tomu, aby vyvolávala pareidolii, ale nesmí být zcela pravidelná. S pomocí matematických metod můžeme sestrojit dokonalé fraktály. Ty ovšem lidský mozek vnímá spíše jako filigrány či mozaiky.

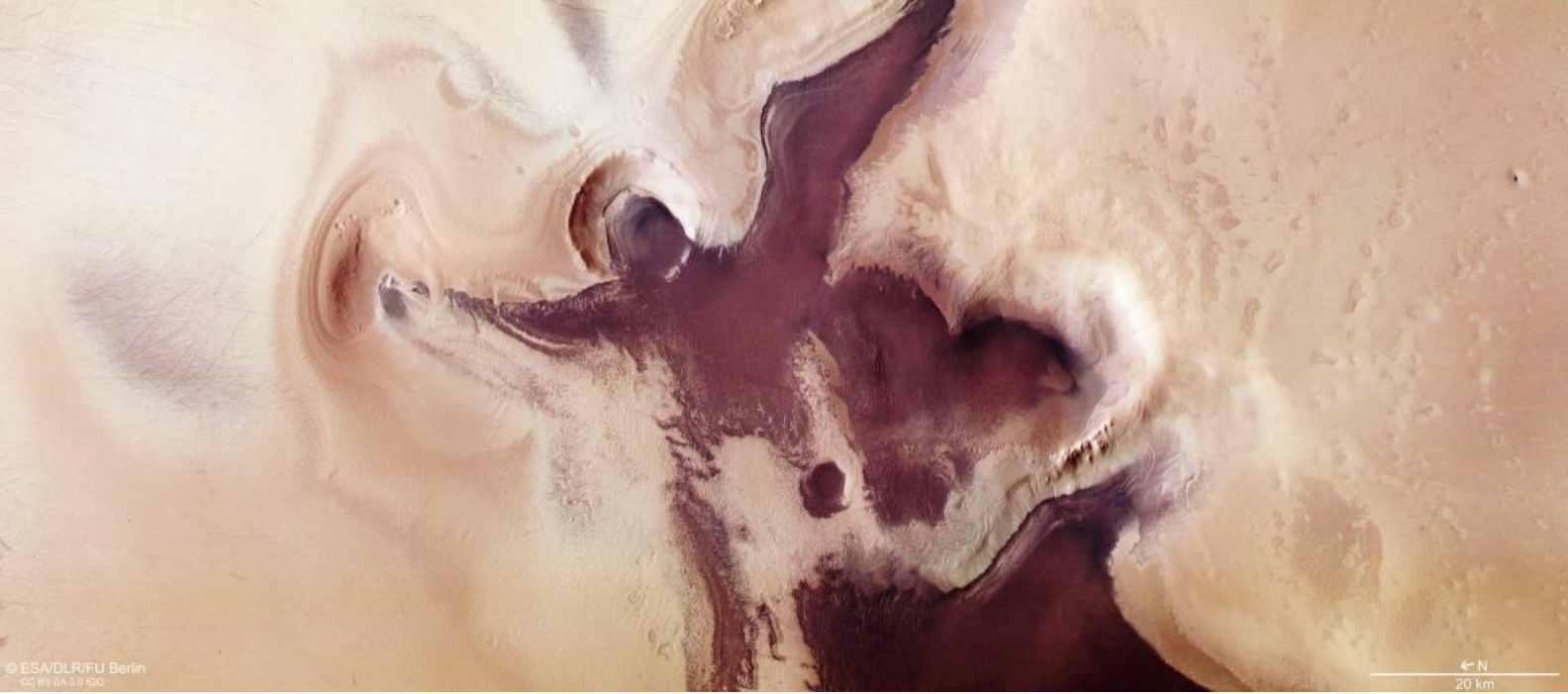Anděl se svatozáří a srdce, jak je letos na rudé planetě zaznamenala kamera sondy Mars Express evropské agentury ESA. Je to výsledek kontrastu barev marsovských dun, které jsou tvořeny písky bohatými na tmavé minerály. | zdroj: ESA

Známé tvary máme tendenci vidět jen ve statistických fraktálech. Tedy takových, u kterých se na různých úrovních opakují pouze statistické vlastnosti tvaru. Přesně takové vlastnosti má řada přírodních útvarů i uměleckých děl. K tomu, aby vyvolávaly pareidolii, ale musí splňovat ještě další požadavky.

Oblaka jsou pro naši fantazii požehnáním

Podle analýzy prezentované v odborném časopisu PLoS ONE jsou klíčové zejména kontury objektů a jejich fraktální rozměry. Nízké hodnoty této veličiny jsou charakteristické pro velké jednolité skvrny. Stoupající fraktální dimenze se vyznačuje zvyšující se roztříštěností tvarů a růstem jejich počtu, přičemž u opravdu vysokých hodnot nejsou obrázky rozeznatelné od zrnění.

Výzkumníci nejprve vytvořili na počítači náhodné černobílé skvrny s různými hodnotami fraktální dimenze a následně je ukazovali dobrovolníkům, kteří si je měli dobře prohlédnout a nahlásit, kolik různých tvarů by v každém obrázku dokázali pojmenovat – jako u Rorschachova testu.

Ukázalo se, že největší míru pareidolie vyvolávají útvary s nízkou fraktální dimenzí. Tedy takové, které sestávají z několika větších skvrn. Pokud ovšem útvary zjednodušíme až moc a fraktální strukturu úplně odstraníme – okraje útvarů vyhladíme – podnětnost útvarů jako mávnutím kouzelného útvaru zmizí. Pro náš mozek se stanou jen nudnými fleky.

Jak ukázala další analýza, originální černobílé Rorschachovy skvrny vykazují v tomto ohledu takřka ideální vlastnosti. Ze stejných důvodů v nás největší pareidolii vyvolávají oblaka a podobné útvary s roztrhanými okraji, například některá skaliska, anebo oheň, ze kterého šlehají plameny. Jasnou souvislost mezi hodnotou fraktální dimenze a množstvím různých interpretací jednotlivých Rorschachových skvrn potvrdil i pohled do psychologických databází.

Skála v Bretani, ve které můžete vidět Apače. | zdroj: tisková zpráva

O něco hůř dopadly Rorschachovy členitější obrazy se soustavami barevných skvrn. Ty ale může mozek ze zjevných důvodů vnímat poněkud odlišně. Svou roli také zřejmě hraje dvojstranná souměrnost útvarů. Fraktální dimenze ale v každém případě hraje klíčovou roli.

Pomůžeme tím robotům?

Náš mozek je očividně nastavený na fraktální povahu většiny přírodních útvarů. Pareidolii nápadně nahrávající hodnoty fraktální dimenze mají i některé typy zvířecího maskování.

Zdá se tak pravděpodobné, že fraktální tvary sehrály svou roli i v evoluci obrany proti predátorům a že pareidolií oplývá nejen člověk, ale také většina zvířat s dostatečně velkým mozkem.

Má výzkum pareidolie také nějaké praktické využití? Překvapivě ano. I když necháme stranou nejrůznější formy umění, aplikace podobných "estetických" studií mohou být překvapivě široké. Už dnes se například mluví o nových typech bojové kamufláže.

Pochopení toho, jak mozek vnímá a interpretuje okolní svět, navíc představuje nezbytný krok při vývoji robotů schopných učení a orientace v prostoru, nebo programů schopných automaticky identifikovat různé tvary nebo obrazy.

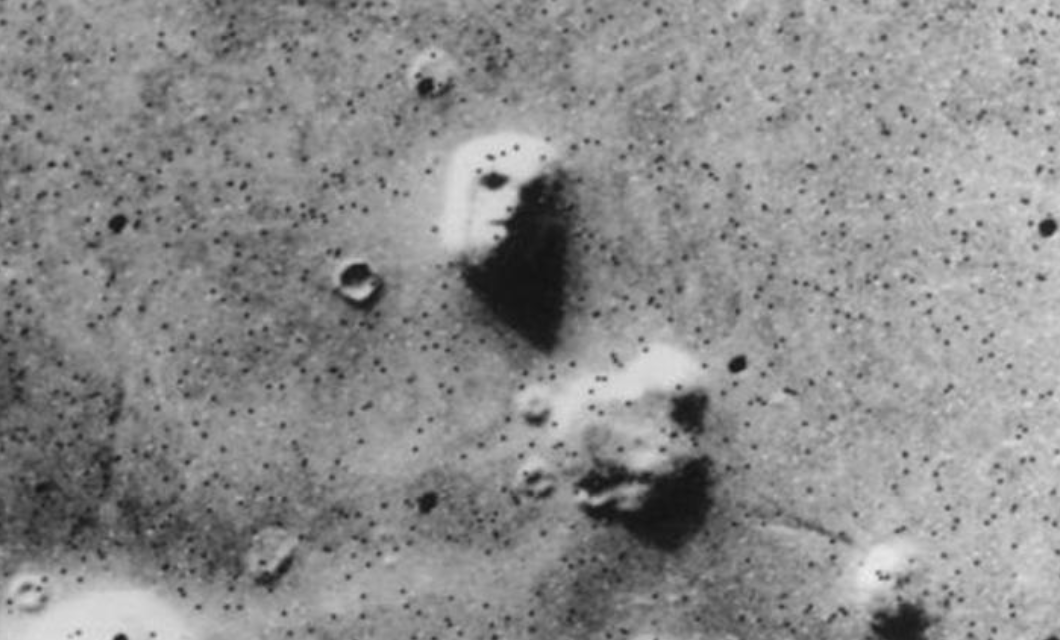A ještě jednou Mars. Lidská hlava? Jen hra světla a stínů. Když nám v roce 1976 poslala sonda Viking 1 rozmazaný snímek marsovské oblasti Cydonia, podnítila teorie o vyspělé civilizaci, která zvládla doletět na Mars a zpět a potom zanikla. | zdroj: tisková zpráva

Zdroj: RP Taylor, TP Martin, RD Montgomery, JH Smith, AP Micolich, C Boydson, BC Scannell, MS fairbanks & B Spehar (2017): Seeing shapes in seemingly random spatial patterns: Fractal analysis of Rorschach inkblots. PLoS ONE 12.